总览
本篇文档介绍了如何将四叉树(QuadTree)空间表示法与**模型预测控制(MPC)**集成,用于复杂环境下的机器人路径规划。
该架构的优势在于:
- 四叉树 提供了适应环境复杂度的空间划分与凸包区域
- MPC 可在动态、带约束的前瞻性框架下生成最优控制
核心思想是:将四叉树节点生成的凸包区域转化为线性不等式约束,供 MPC 在轨迹优化中使用,完成避障与路径限制。
架构图
环境地图 ────► 四叉树分解 ────►凸包生成
│
▼
机器人控制 ◄──── MPC优化器 ◄────线性几何约束
四叉树地图表示
四叉树将环境划分为不同分辨率的空间单元:
- 开放区域使用较大的节点
- 障碍物附近使用更小的细节节点
- 仅保留表示自由区域的叶子节点
优势
- 自适应分辨率:按需细化,避免资源浪费
- 内存友好:比统一网格更节省存储
- 支持多分辨率路径规划
凸包区域构建
四叉树分解完成后:
- 将每个自由叶子节点看作不规则区域
- 为每个叶子节点生成一个凸包(Convex Hull)
- 这些凸包表示机器人可以安全通行的区域
- 邻接凸包间连接形成路径图
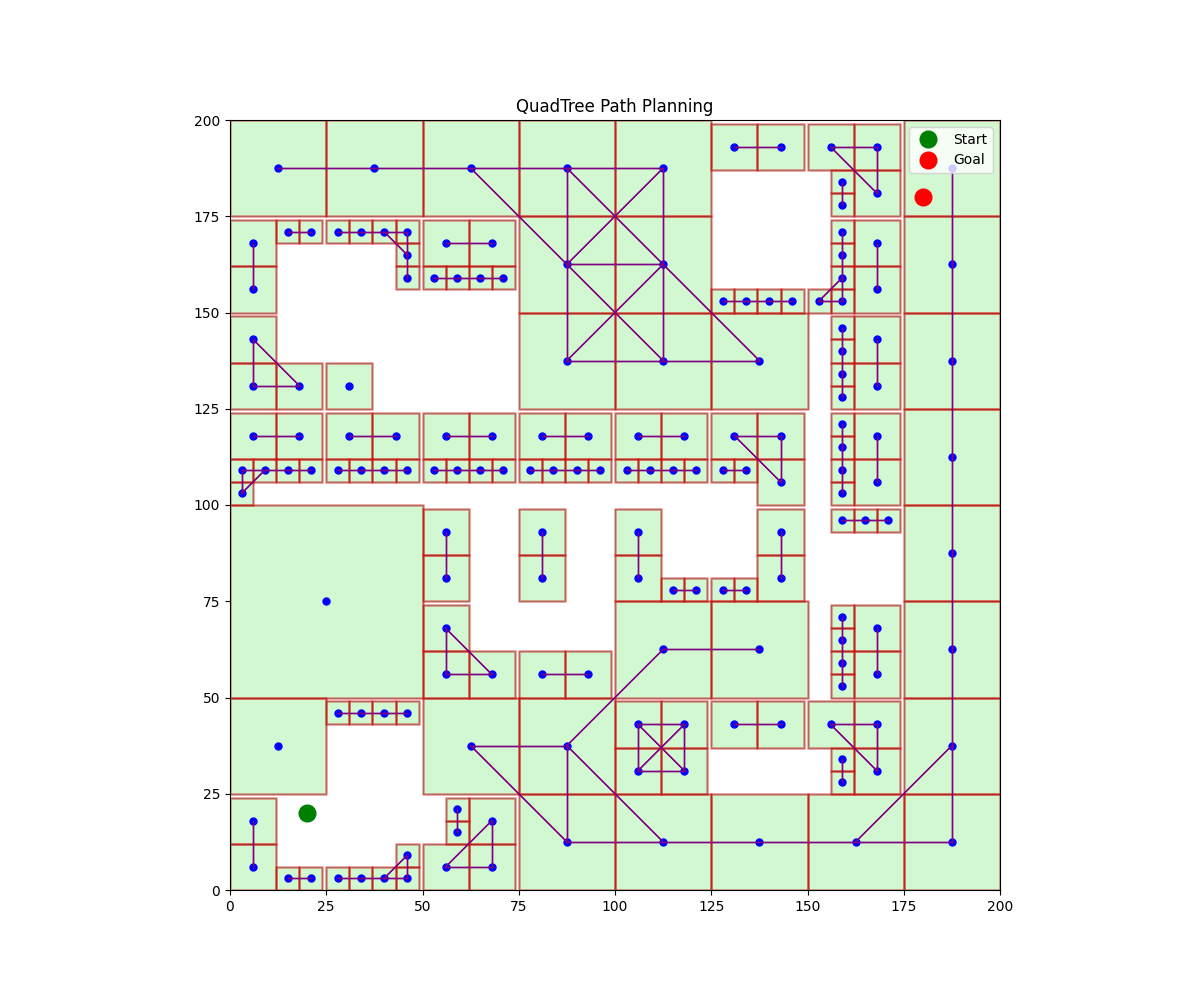
MPC 所需的约束生成方式
对于路径经过的每个凸包区域:
- 凸包每条边转化为半空间线性约束
ax + by + c ≤ 0 - 约束的法向量需朝向凸包外部
- 保证 MPC 优化轨迹始终在凸包(安全区)内
数学上,对于边 (x₁,y₁) → (x₂,y₂):
a = -(y₂ - y₁)
b = (x₂ - x₁)
c = -ax₁ - by₁
约束形式为:ax + by + c ≤ 0
MPC 优化器与四叉树约束集成
MPC 优化问题形式:
min J = Σ (x - x_ref)^T Q (x - x_ref) + u^T R u
s.t.
x_{k+1} = f(x_k, u_k) # 系统动力学
u_min ≤ u ≤ u_max # 控制约束
ax + by + c ≤ 0 (凸包边界线性约束)
变量说明:
- x:机器人状态(位置、朝向)
- u:控制输入(速度、角速度)
- x_ref:参考轨迹
- Q, R:加权矩阵
动态障碍物支持
该方法对动态障碍具有较强适应性:
- 障碍物发生移动 → 仅更新受影响的四叉树节点
- 对这些节点重新生成凸包
- MPC 重新接收新的约束更新未来轨迹
相比全局重规划效率更高。
实现步骤
1. 从环境地图生成四叉树
occupancy_grid = create_occupancy_grid()
quadtree = QuadTree(occupancy_grid, min_cell_size=4)
2. 对每个自由节点生成凸包
for node in quadtree.leaf_nodes:
if node.is_free():
hull = ConvexHull(node.vertices)
convex_hulls[node.id_sequence] = hull
3. 使用 A* 搜索路径节点
path_nodes = quadtree.find_path(start_pos, goal_pos)
4. 将路径节点对应的凸包边转化为线性约束
static_constraints = []
for node_id in path_nodes:
hull = quadtree.convex_hulls[node_id]
vertices = hull.points[hull.vertices]
for j in range(len(vertices)):
start, end = vertices[j], vertices[(j+1)%len(vertices)]
dx, dy = end[0]-start[0], end[1]-start[1]
length = np.sqrt(dx**2 + dy**2)
a, b = -dy/length, dx/length
c = -(a*start[0] + b*start[1])
static_constraints.append((a, b, c))
5. 将约束注入 MPC 控制器
mpc.update_static_constraints(static_constraints)
性能考虑
- 初始化快:四叉树预处理只需执行一次
- 运行高效:MPC 每步仅考虑路径上的区域约束
- 适配动态场景:仅局部更新受影响节点
拓展方向
- 融合预测轨迹 → 对未来障碍行为做预测修正
- 基于距离做分辨率动态调整
- 融合强化学习 → 动态调节权重、路径选择等参数
总结
此方法有效结合了:
- 四叉树高效地图表示
- 凸包转线性约束方式
- MPC 的鲁棒前瞻控制
可广泛应用于复杂、动态、高密度环境下的机器人轨迹优化问题。
示例代码片段:预测约束生成
def generate_predicted_constraints(obstacle_trajectory, horizon=10):
constraints_over_horizon = []
for t in range(horizon):
predicted_pos = obstacle_trajectory.predict(t)
constraint_t = generate_constraint_from_obstacle(predicted_pos)
constraints_over_horizon.append(constraint_t)
return constraints_over_horizon